Методические основы уровневой дифференциации при обучении алгебре в классах с углубленным изучением математики
После преобразований получим
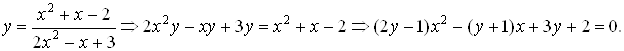 Для того, чтобы уравнение имело решение необходимо и достаточно, чтобы
Для того, чтобы уравнение имело решение необходимо и достаточно, чтобы

Отсюда наименьшее значение функции 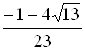 , наибольшее
, наибольшее 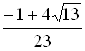 .
.
Ответ:

Как видно из решений последних задач на нахождение наибольшего и наименьшего значений иногда удобнее рассматривать функцию ![]() как уравнение с неизвестным
как уравнение с неизвестным ![]() , в котором необходимо установить при каких
, в котором необходимо установить при каких ![]() это уравнение имеет решение. Рассмотрим еще один пример, в котором работает эта идея с небольшими вариациями.
это уравнение имеет решение. Рассмотрим еще один пример, в котором работает эта идея с небольшими вариациями.
16. Найти наибольшее и наименьшее значение выражения ![]() , если
, если
![]() .
.
Решение.
Положим ![]() . Подставим полученное выражение в (1):
. Подставим полученное выражение в (1):

Ответ: наибольшее значение выражения ![]() равно
равно ![]()
![]() ; наименьшее -
; наименьшее - 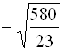 .
.
Рассмотрим один из самых универсальных методов доказательства – методом математической индукции.
17. Доказать, что при любом натуральном ![]() число
число ![]()
![]() делится на 7.
делится на 7.
Решение.
Обозначим ![]() .
.
При ![]()
![]() - делится на 7.
- делится на 7.
Пусть ![]() делится на 7.
делится на 7.
Имеем 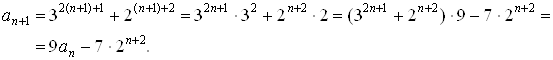
Последнее число делится на 7, т.к. представляет собой разность двух целых чисел, которые делятся на 7, ч.т.д.
17. Доказать тождество:
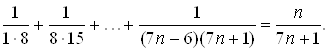
Решение.
1)При ![]()
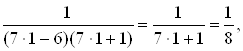 равенство выполняется.
равенство выполняется.
2)Предположим, что равенство выполняется при ![]()
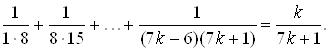
При ![]() имеем:
имеем:
