имеет решения.

Процесс нахождения дискриминанта и доказательства, что он положителен достаточно трудоемкий, поэтому попробуем другой метод решения.

Пусть .

при любом .

Т.о. уравнение всегда имеет решение, причем если , то уравнение имеет два корня; при этом всегда имеется корень, удовлетворяющий неравенству .

12. Пусть и корни уравнения . Выразить через и .

Решение.

Необходимо выразить через и :

По теореме Виета

тогда

Ответ: .

13. Определить все значения параметра , при которых уравнение имеет 1 корень.

Решение.

В условие не сказано, что рассматривается квадратное уравнение, поэтому рассмотрим случай

Остальные значения параметра получим из уравнения .

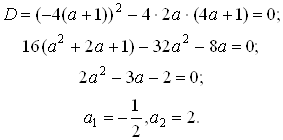
Ответ: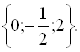

Простейший прием нахождения наибольших значений, основанный на свойствах квадратичных функций состоит в том, что исследуемая функция при помощи преобразований или замены переменной приводится к квадратичной, после чего выделяется полный квадрат.

14.Найти наибольшее значение функции

Решение.

Положим , тогда Отсюда Итак, после замены получим, что надо найти наибольшее значение

15.Найти наибольшее и наименьшее значения функции .

Решение.

Рассмотрим данное неравенство как уравнение с неизвестным и параметром .